
The Circle of Fifths is a useful tool, with the 12 keys in music arranged in the fifth degree of each other on a circle, in a clockwise fashion, and in the fourth degree of each other in a counter-clockwise fashion.
The Circle of Fifths can help you quickly access information such as what are the notes and chords in a specific key, where are the sharps and flats, as well as transposing between keys with ease.
In this 2 part series article, you’ll learn about the 16 ways in which you can put the Circle of Fifths to use.

1. 12 Major, Minor, and Their Relative Keys
At first glance, you can easily see the 12 major keys laid out in the outer circle (C, G, D, A, E, B, G flat, D flat, A flat, E flat, B flat, F), and the 12 minor keys in the inner circle (Am, Em, Bm, F#m, C#m, G#m, Ebm, Bbm, Fm, Cm, Gm, Dm).
For relative keys, each major key on the outer circle would correspond to a relative minor key on the inner circle. For example, a relative minor key to C major would be A minor, and a relative major key to F minor would be A flat.
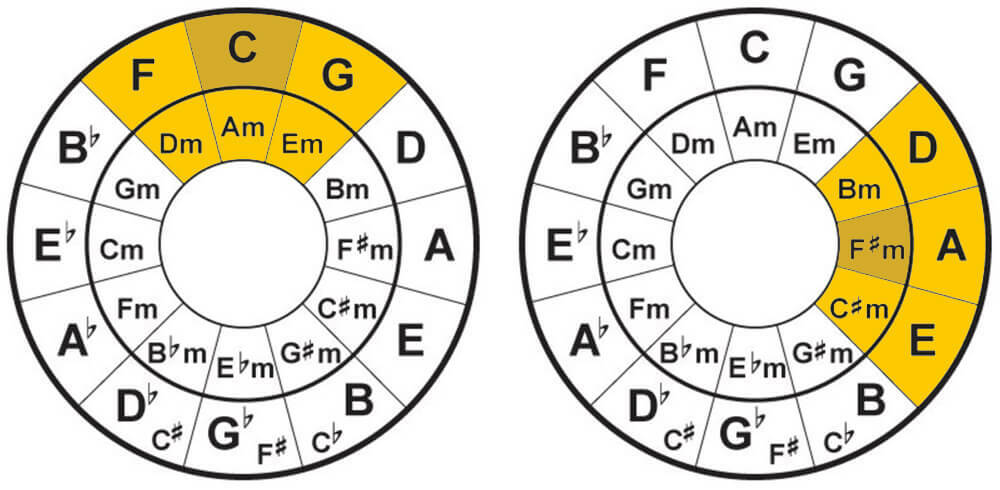
2. Chords in a Key
The Circle of Fifths can help you determine the chords that are contained within a specific key by looking at the ‘grouping of six’ surrounding the specific key.
Using C major as an example, to find its group of six, use C major as the center. Together with the 5 keys surrounding it, you’ll get the six chords within the C major key (C major, F major, G major, A minor, D minor, and E minor).
Likewise, if you want to figure out the chords in the F#m key, use F#m as the center, and together with the 5 keys surrounding it, you’ll get the six chords that are within the F#m key (F#m, Bm, C#m, A, D, E).
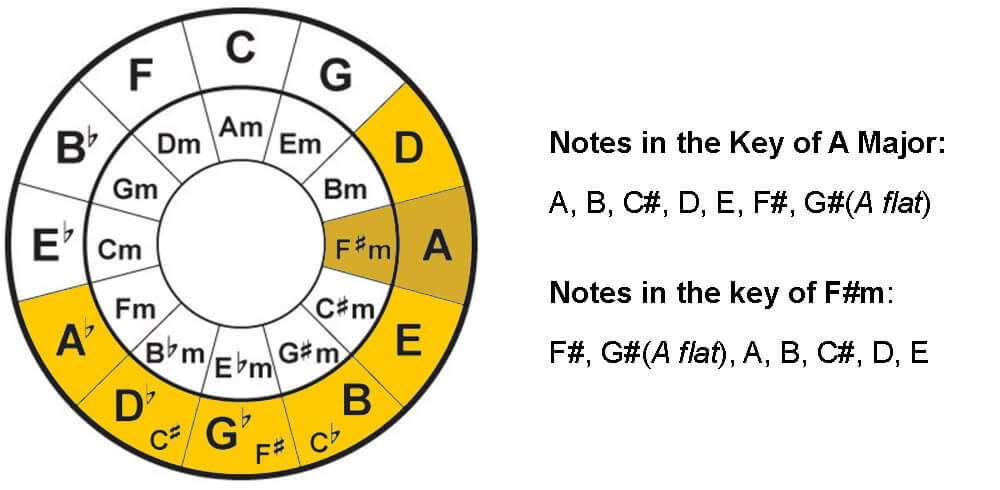
3. Notes in a Key
To find the notes in each key, you need to understand something called the ‘Enharmonic Equivalent’, which is a note that is equivalent to another note, but in a different name.
So looking at the diagram, using A major as an example, the formula for identifying the notes is to take the first note in the counter-clockwise direction of A, and the subsequent 5 notes in the clockwise direction.
Hence, the notes in the Key of A major would be A, B, C#, D, E, F#, G#(A flat).
At this point, you’re probably a little confused as there is no G# on the Circle of Fifths chart. This is the enharmonic equivalent concept mentioned at the beginning of this section. G# is another name for A flat, just like D flat is another name for C#, and G flat is another name for F#.
For relative keys, the 7 notes are the same. Meaning, that the 7 notes in a key of F#m are exactly the same notes as those in the key of its relative key A major. Hence the notes in the key of F#m are F#, G#(A flat), A, B, C#, D, E.
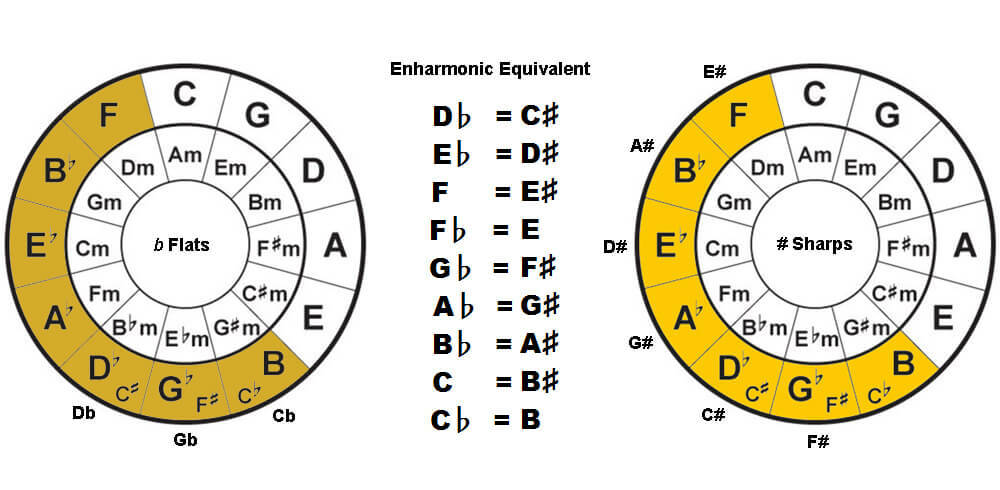
4. "Sharp Keys" vs. "Flat Keys"
If you’re wondering at this point why are the notes called sharps in some instances and flats in others, the Circle of Fifths chart comes in useful again.
When looking at the keys and notes on the circle, the right side is comprised of sharps, while the left side is comprised of flats. Hence, any notes that fall on the right side will be referred to as ‘sharps’, and the ones falling on the left side will be referred to as ‘flats’.
In middle, you have the key of C major and A minor at the top, and the key of G flat and F# at the bottom.
Notes in the key of C major and A minor do not contain any flats or sharps, hence their notes will always be A, B, C, D, E, F, and G.
Notes in the key of G flat and F# however, each can contain 6 flats or 6 sharps. Depending on what key they’re in, a flat or sharp note will be used in accordance to the enharmonic equivalent.
For example, if you’re in the key of G flat, then your notes will be in flats (Gb, Ab, Bb, Cb, Db, Eb, F). And if you’re in the key F#, then your notes will be in sharps (F#, G#, A#, B, C#, D#, E#).
Same position, same notes. Just different names.
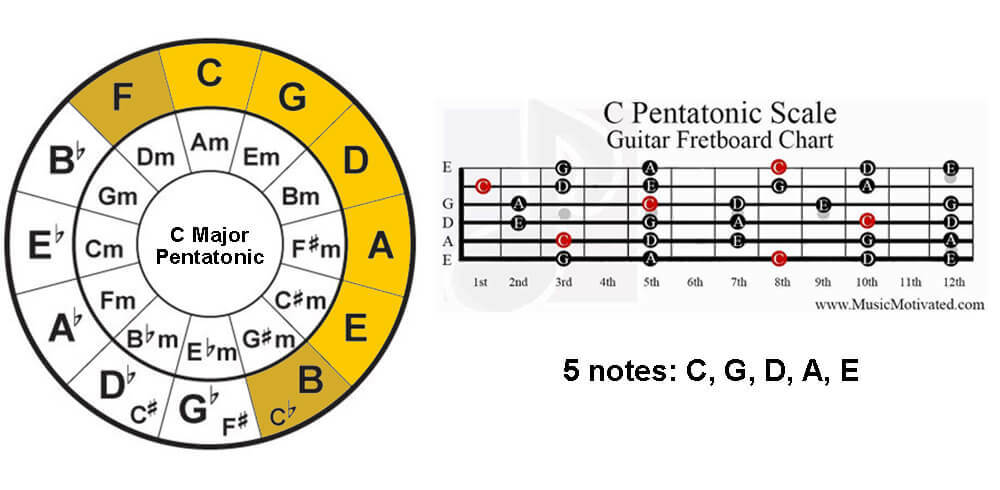
5. The Pentatonic Notes
You may have heard a lot about pentatonic scales and how they are the bedrock of improvisation and creation. In order to practice each of the major and minor pentatonic scales, you’ll need to know what the notes are.
By using the Circle of Fifths, you can easily find out what the notes are for each of the major and minor pentatonic scales.
In the case of a C major pentatonic scale, locate the C note on the Circle of Fifth, together with the subsequent 4 notes in its clockwise direction you’ll have your 5 notes of the C major pentatonic scale.
Alternatively, you can also refer to the 7 notes of the C major key on the Circle of Fifths, and simply remove the first note (F) and last note (B) to get the 5 notes for the C major pentatonic scale.
The same method applies to finding the notes for the pentatonic scales. Simply start with the base note you want, and include the immediate 4 notes in the clockwise direction.
For minor scales, like notes in the major keys, the same rule applies to notes in a pentatonic scale. Each set of major and minor relative keys share the same pentatonic notes, C major pentatonic scale shares the same notes with A minor pentatonic scale, D major pentatonic scale shares the same notes with B minor pentatonic scale, and so on and so forth.
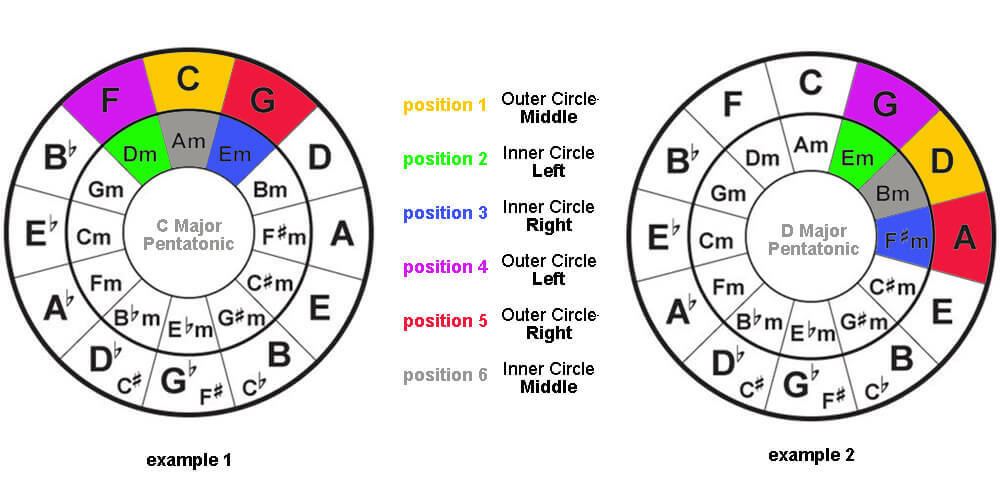
6. Numbering Chord Progressions
When you’re talking about chord progressions, essentially you’re talking about the sequence in which the chords of a specific key are being played in a piece of music.
Let’s take the key of C major as an example, we have the chords C, G, F, Dm, Am, and Em. And assuming you’re going to play a common chord progression 1, 5, 6, 4. You can then use the Circle of Fifths to figure out which of the 6 chords are in what position and play the 1, 5, 6, 4 chord progression accordingly.
The positioning numbers are fixed for every key, hence by using the grouping of six in example 1 of the diagram, you can figure out that the numbered position for notes in a C major key is #1-C, #2- Dm, #3- Em, #4-F, #5-G, and #6-Am.
So by playing the chord progression of 1, 5, 6, and 4, you’ll be playing C, G, Am, and F in terms of chords.
Likewise in example 2, if you’re playing the same chord progression 1, 5, 6, and 4 in the key of D major, the chords you’ll play in this progression will be D, A, Bm, and G.
Now if you have a guitar handy, go ahead and play the chord progression in the above examples, you will realize that they both sound the same, except in a different key. And this is exactly how you can transpose a piece of music from one key to another.
I hope the 6 applications above have shed some light on how easy and useful the Circle of Fifths can be when it comes to playing the guitar.
This is a 2 part series, be sure to come back for the second part where you’ll learn 10 more Circle of Fifths applications that you can put to use right away.
Rock On nn/,
Related Resources:
Guitar Chord Progressions and the Number System Explained







