
In part one of the Circle of Fifths series, you’ve learned how to use the Circle of Fifths to find the relative keys for each major and minor scale, the chords and notes of each key, sharpened and flatted keys, the pentatonic scale for each key, and the numbering for chord progressions.
If you haven’t read part one, I suggest you read it first before continuing with part two as it contains many fundamentals of the Circle of Fifths, which will make part two a lot easier to understand.
In this part 2 of the Circle of Fifths series, because certain topics can get a little complex, hence it’s broken into 2 sections, 2a and 2B, for easy learning.
In the first section, 2A, you’ll first learn how to use the Circle of Fifths to easily find:
Finding The Diminished Chord on the Circle of Fifths
Find the Triad Notes of a Chord on the Circle of Fifths
Know How Many Sharps or Flats There Are Using the Circle of Fifths
Determine Which Notes are Sharp or Flat Using the Circle of Fifths
And in the second section, 2B, we’ll dive a little deeper into some music theory where you’ll learn to use the Circle of Fifths to find:
Finding Dominant Chords Using the Circle of Fifths
How to Find the 7 Modes Using the Circle of Fifths
Using Circle of Fifths to Identify Modes from the Brightest to the Darkest Sound
Using Circle of Fifths to Find Borrowed Chords
Using Circle of Fifths to Identify Music Intervals
Using Circle of fifths to Identify Reciprocal Intervals
Let’s begin!
Finding The Diminished Chord on the Circle of Fifths
In part 1 of this series, you learned how to find the chords of a major key through the ‘grouping of six’.
But you might be wondering shouldn’t there be 7 chords in a key?
And you’ll be right, there is a 7th chord in each key, just like there is a 7th note in each key. But to keep things simple in the first part, we’ll talk about it individually today in part 2.
In every key, there are 7 diatonic chords. Diatonic chords are chords formed using the native notes of a key. For example, the C major chord is a diatonic chord of the C major key because it’s formed using the notes C, E, and G, which are native notes to the key of C major.
Likewise, the A major chord is the diatonic chord of the A major key because it’s formed using the notes A, C#, and E, which are native notes to the key of A major.
In each key, the 7 chords are made up of 3 major chords, 3 minor chords and the 7th chord, the diminished chord.
So what is the 7th chord and how do you find it?
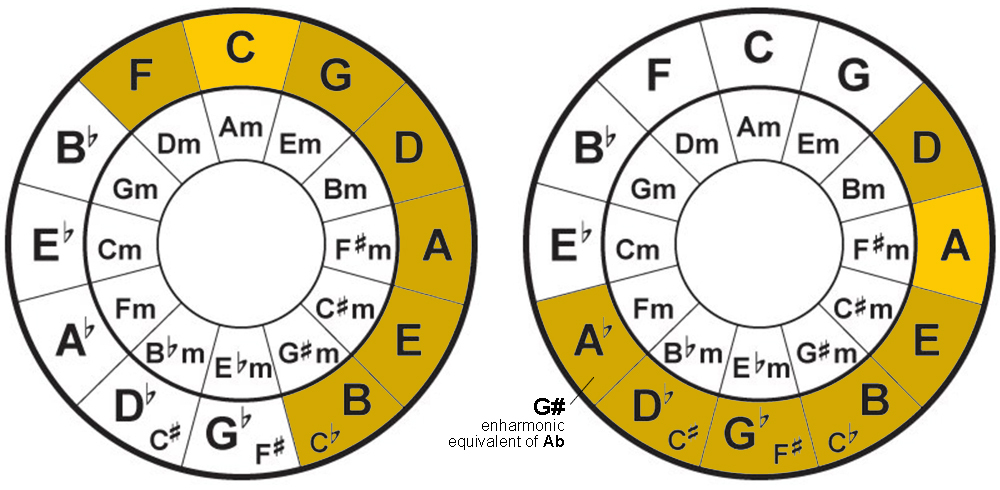
Looking at the Circle of Fifths, using C major key as an example, your 3 major chords are C major, F major, and G major (outer circle). And your 3 minor chords are D minor, A minor, and E minor (inner circle).
As for the 7th chord (diminished chord), just like finding the notes of a key, you start by taking the first note in the counter-clockwise direction of the root key C, and you’ll get F. And in the clockwise direction, count to the 7th-degree note, which is B, and that is your 7th chord. B Diminished (Bdim).
Likewise, to find the 7th chord in the A major key, start by taking the first note in the counter-clockwise direction of the root key A, which is D, and count to the 7th-degree note in the clockwise direction, which is G#/Ab. And since you’re basing your 7th chord on the key of A major (on the right side of the circle), therefore your 7th chord would be G# Diminished (G#dim).

Find the Triad Notes of a Chord on the Circle of Fifths
If you don’t know what a triad is, it’s simply the 3 notes that make up a chord. For example the triad notes for a C major chord are C, E, and G. And for the A minor chord they’re A, C, and E.
When you write the notes of a key out, triads are the first, third and fifth note of that key. 1, 3, 5, of the C major key is C, E, and G. 1, 3, 5, of the A minor key is A, C, and E.
But there’s a faster way to spot these triads on the Circle of Fifths, you’ll need to look out for the triangular pattern.
For triads in the major scale, the triangular pattern is consist of the root note, the note 1 degree clockwise to the root note, and the note below the second note (inner circle).
In the case of a C major chord, the root note is C. The note clockwise to its right is G, and the note below G, in the inner circle is E.
Likewise, the triad for A flat major is its root note Ab, the note clockwise to its right is Eb, and the one note below Eb in the inner circle is C. Thus, the triads for A flat major are Ab, Eb, and C.
For triads on the minor scale, the triangle pattern consists of the root note, one note clockwise to its right, and the relative note to the root note in the outer circle.
So for the A minor chord, the triad is its root note A, one note clockwise to its right is E and its relative note in the outer circle is C. Hence the triads for the A minor chord are A, E, and C.
Let’s talk about G# minor chord. For the triads for G# minor chord, using the triangular pattern you’ll find G#, D#, and B. But in this instance, the reason you’re using a D# instead of its enharmonic equivalent Eb, is because it’s a sharpened chord.
Know How Many Sharps or Flats There Are Using the Circle of Fifths
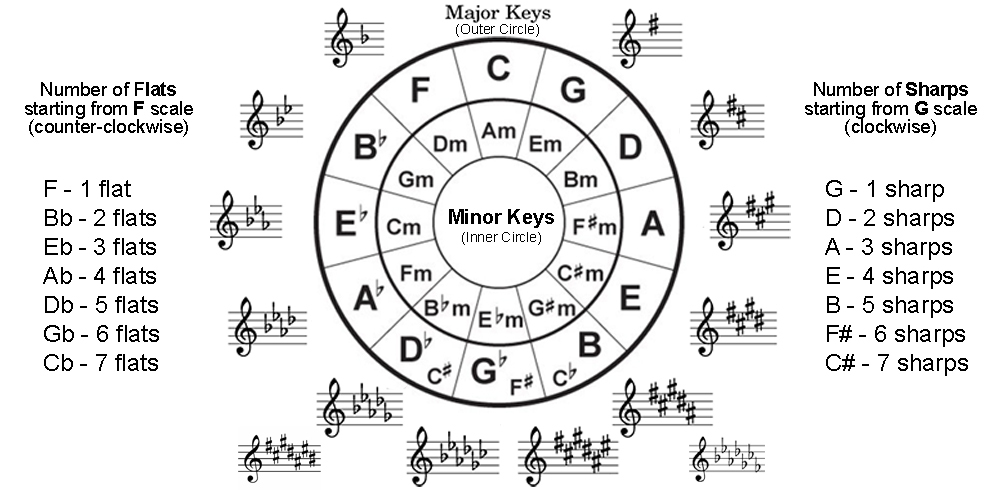
Based on the positions of each key on the Circle of Fifths, you are able to tell how many sharpened and flatted notes are in each key.
Since the C major key and A minor key are neutral with no flats and sharps, you will count the sharps on the right side of the circle starting with the key of G. And count the flats on the left side of the circle starting with the key of F.
On the right side (sharps), starting with the key of G you’ll have 1 sharp. And with every subsequent key, you’ll add another sharp to it. So in the key of D, you’ll have 2 sharps, and in the key of A, you’ll have 3 sharps. When you arrive at C#, you should have 7 sharps.
For flats, you start on the left side of the circle with the key of F, abiding by the same rule of adding a flat in each key counter-clockwise. So for the key of F, you’ll have 1 flat, for the key of Bb it has 2 flats, so on and so forth. And when you get to the key of Cb, you’ll have 7 flats.
Determine Which Notes are Sharp or Flat Using the Circle of Fifths
Continuing on the subject of determining sharps and flats, how do you determine which notes in a key are sharps and which notes are flats?
Apart from the Circle of Fifths, you’ll need to know one other thing, which is the Order of Sharps and the Order of Flats.
A side note, the Order of Sharps and Flats is probably the one thing you truly have to memorize because once you do, you will be able to construct the Circle of Fifths from memory.
And once you have constructed the Circle of Fifths, everything taught here can be easily retrieved with ease. Check out our post on Instagram for a quick review of ‘How To Memorize the Circle of Fifths With Ease’.
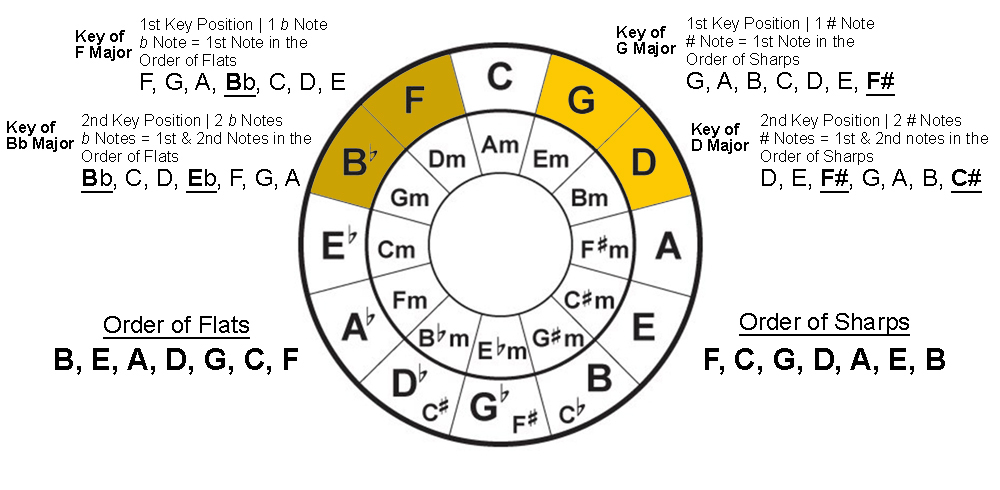
So, the Order of Sharps is as follow in the order of F, C, G, D, A, E, and B.
And to determine what the sharpened notes are in each key, just remember the key that has 1 sharpened note, it’ll be the first note in the Order of Sharps. The key with 2 sharpened notes, it’ll be the first and second notes in the order of sharps.
Now looking at the Circle of Fifths, the first key that contains a sharpened note is G major, and since it’s the first key, it’ll contain 1 sharpened note. Applying the above logic, the sharpened note in the key of G major is F#.
The second key in the clockwise direction is D major. And since it’s in the second key, it’ll contain 2 sharpened notes. Applying the logic of the Order of Sharps, the 2 sharpened notes in the key of D major are F# and C#.
Now let’s take a look at the Order of Flats and its order as follow, B, E, A, D, G, C, and F. To make things easier, just remember that the Order of Flats is the Order of Sharps backward.
And the way to determine what the flatted notes are, the same rule applies but in a counter-clockwise direction.
Starting from the left side of the circle with the key of F, you’ll have 1 flat. The key of Bb will have 2 flats, and the key of Eb will have 3 flats. All the way to Cb where you’ll have 7 flats.
Now apply the same logic as you did in sharps, the key of F is in the first position, hence it has 1 flatted note. Based on the Order of Flats, the flatted note in the key of F is Bb.
For the key of Bb, it’s the second key position and has 2 flatted notes. Using the Order of Flats, the flatted notes in the key of Bb are the first 2 notes, Bb and Eb.
As you can see, the Circle of Fifths is a very convenient tool to retrieve information from quickly. If you can, I would like you to try and construct the Circle of Fifths from memory, using the Order of Sharps and Order of Flats.
In the next section, we will talk a little more about modes and intervals, and truly put the Circle of Fifths to full use.
Rock On nn/,





