
In the first section of part 2, you’ve learned to use the Circle of Fifths to find:
The Diminished Chord on the Circle of Fifths
The Triad Notes of a Chord on the Circle of Fifths
How Many Sharps or Flats There Are Using the Circle of Fifths
Which Notes are Sharp or Flat Using the Circle of Fifths
If you haven’t read it yet, go ahead and read it first and then come back to continue with today’s section, where you’ll learn more applications for the Circle of Fifths.
Using the Circle of Fifths to find Dominant Chords
Using the Circle of Fifths to Identify Modal Scales (Modes)
Arrange Modes from Brightest to Darkest Sound
Using the Circle of Fifths to find Borrowed Chords
Using the Circle of Fifths to find Intervals
Using the Circle of Fifths to find Reciprocal Intervals
Let’s dive into today’s topic!
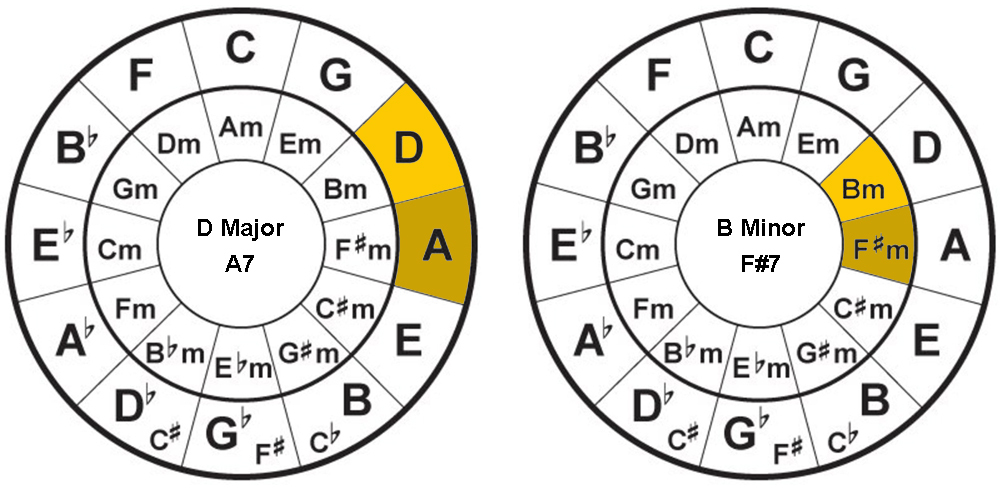
Using the Circle of Fifths to find Dominant Chords
Dominant chords (also known as the dominant 7th chord) are chords that contain a note followed by the number 7. There’s no major or minor to it. For example, G7, C7, and F#7 are all dominant chords.
To explain it simply, the purpose of a dominant chord is to create a little tension (suspense) before ending it on a major chord. For instance, if you want to add a little tension before ending on the C major chord, then the dominant chord you can play is the G7 chord. Likewise, the dominant chord before ending on the A major chord is an E7 major chord.
Finding dominant chords on the Circle of Fifths is very easy. First, base it on the chord you want to end on (or release the tension to). For example, if you want to end on the D major chord, then your dominant chord would be the note 1 degree clockwise to it, which is an A major chord.
Since there are no major nor minor to a dominant, the chord will just be called A7.
Finding a dominant chord for a minor chord is the same. Say you want to end on the B minor chord, therefore your dominant chord will be the note 1 degree clockwise to it, F#7.
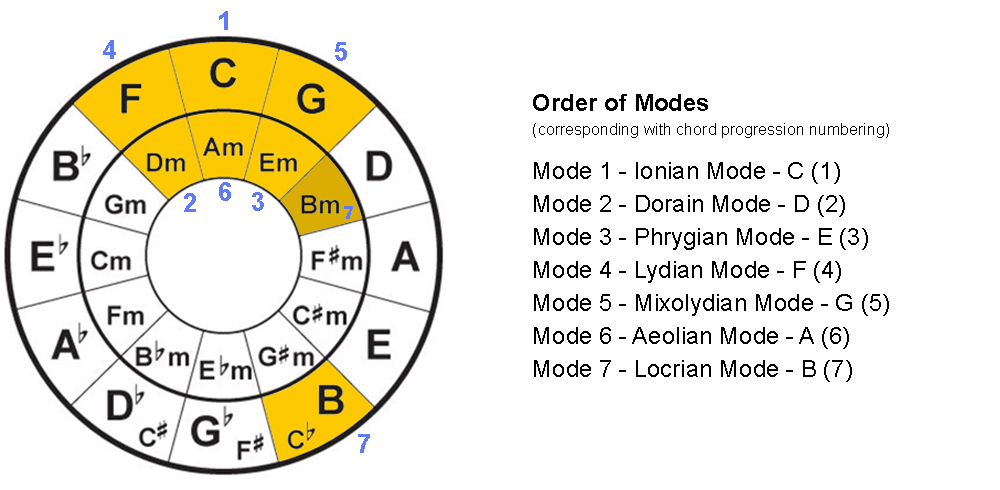
Using the Circle of Fifths to Identify Modal Scales (Modes)
There are in total 7 modal scales, in order from the first mode to the seventh mode they are Ionian, Dorian, Phrygian, Lydian, Mixolydian, Aeolian, and Locrian.
Modal scales (also known as Modes) add new variations and provide a different alternative (sound or feel) to the existing major and minor scales. You can play each of the 7 modes in each of the 12 major scales, which gives you more ways to express your music.
To learn more about modes, visit the link in the related resources section at the end of the page.
With the Circle of Fifths, you can easily remember the order of the modes by using the ‘grouping of six’. In part 1 you learned the numbering of chord progression, from 1 to 6. Using C major as the root, in order of 1 to 6 we have C(1), D(2), E(3), F(4), G(5), and A(6).
And in place of the keys instead, the numbering now represents the order of the modes, Ionian being the first mode, and Locrian being the last. And if you’re being asked to play something in the 4th mode, it means you’ll be playing in the Lydian mode.
Mode 1 – Ionian Mode – C (1)
Mode 2 – Dorain Mode – D (2)
Mode 3 – Phrygian Mode – E (3)
Mode 4 – Lydian Mode – F (4)
Mode 5 – Mixolydian Mode – G (5)
Mode 6 – Aeolian Mode – A (6)
Mode 7 – Locrian Mode – B (7)
You’ve found the first 6 modes using the chord progression sequence, and for the seventh mode, you’ll find it the same way you would with finding your diminished chord, the 7th-degree note from F in the outer, or the 2nd-degree note from Em in the inner circle.
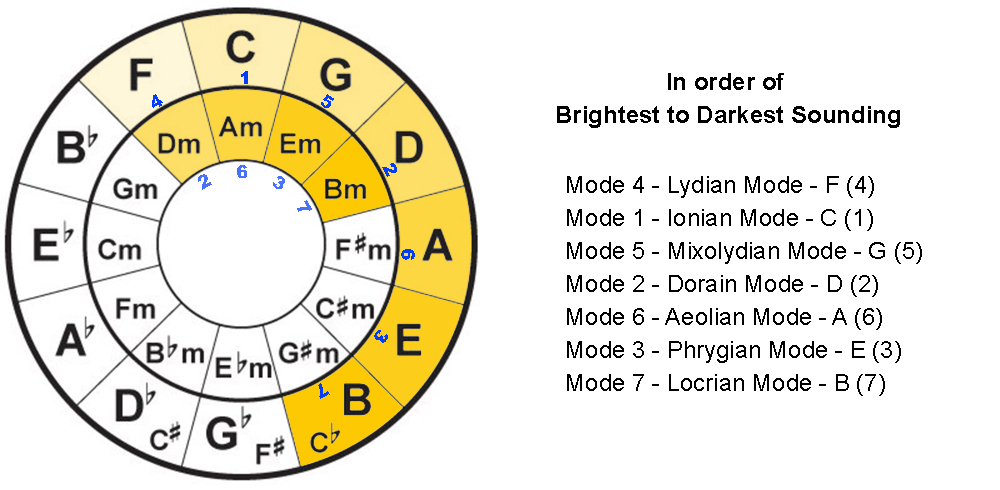
Arrange Modes from Brightest to Darkest Sound
One of the key differences between the modes is that they each carry a unique sound quality, from the brightest to the darkest. Regardless of what key signature you play them in, Lydian mode will always sound the brightest, whereas the Locrian mode will always sound the darkest.
To find the modes in order of their sound quality using the key of C major, from brightest to the darkest we can use the linear method on the outer circle F, C, G, D, A, E, and B. Or the stacked method using the grouping of six.
Mode 4 – Lydian Mode – F (4)
Mode 1 – Ionian Mode – C (1)
Mode 5 – Mixolydian Mode – G (5)
Mode 2 – Dorain Mode – D (2)
Mode 6 – Aeolian Mode – A (6)
Mode 3 – Phrygian Mode – E (3)
Mode 7 – Locrian Mode – B (7)
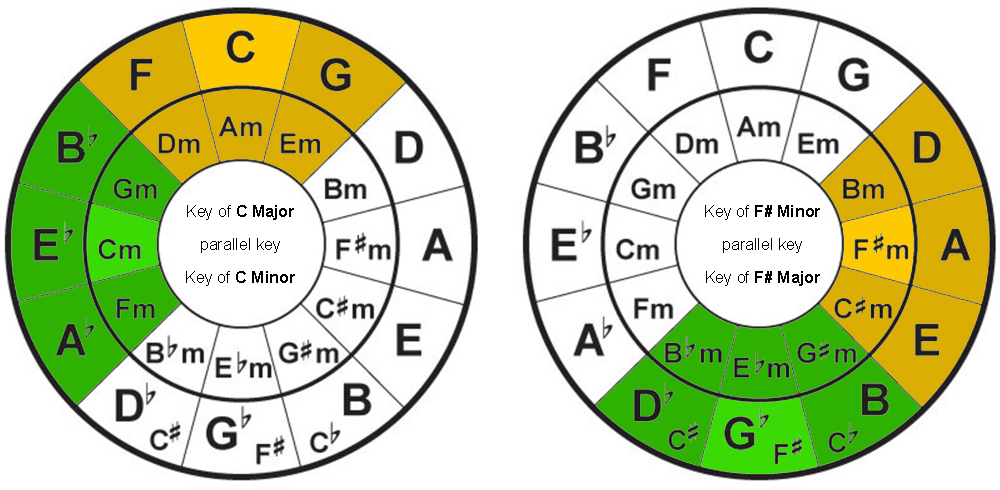
Using the Circle of Fifths to find Borrowed Chords
Another simple way to add variety to your playing is to include chords that are outside of the key you’re playing in, these outside chords are called ‘Borrowed Chords’.
To find the group of borrowed chords that goes well with the key you’re playing, on the Circle of Fifths, look out for the parallel major key or minor to that you’re playing.
For example, if you’re playing in the key of C major, its parallel chord would be C minor. And your group of borrowed chords will be in the group of six based around C minor.
The same rule applies when finding borrowed chords for the other respective keys. Borrowed chords will be from the group of six from the parallel key.
To make sure you understand, let’s try another example.
If you’re playing in the key of F# minor, your borrowed chords will be from the key of F# major. Likewise, if you’re playing in the key of Bb minor, its borrowed chords will be from the key of Bb major. It’s that simple.
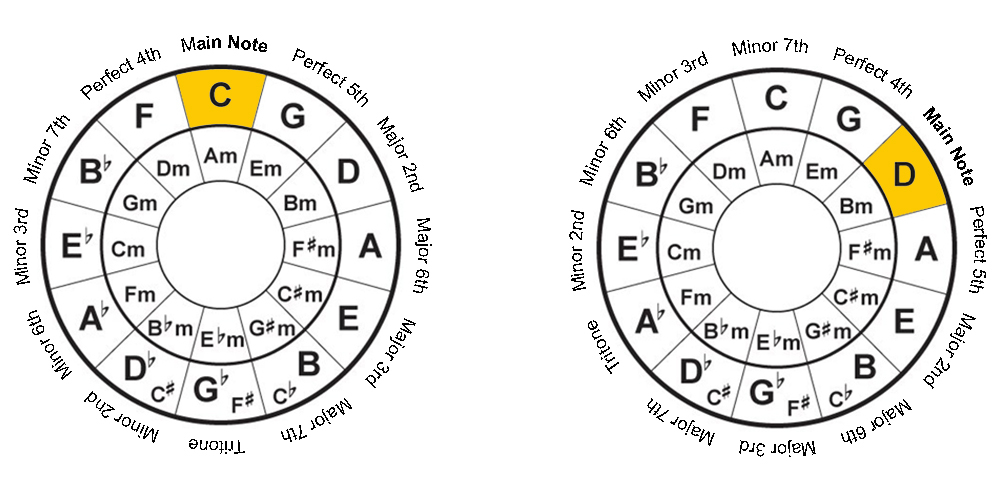
Using the Circle of Fifths to find Intervals
Intervals are a crucial part of learning music as it helps with ear training, allowing you to pick up different pitches by ear, and recognize the difference between 2 notes. So what is an interval?
An interval is simply the distance in pitch between 2 notes.
Each interval has its own name, and you can easily refer to the names and immediately work out the interval between 2 notes on the Circle of Fifths by following a fixed formula illustrated in the diagram.
Using C as an example for your main note, you’ll see the names of different intervals going in both clockwise and counter-clockwise directions from C.
In the clockwise direction, you have the intervals Perfect 5th, Major 2nd, Major 6th, Major 3rd, Major 7th, and finishing on an interval called the Tritone, which is always directly opposite of the main key, because it’s the furthest interval from your main note.
Going in the counter-clockwise direction, the intervals in order are Perfect 4th, Minor 7th, Minor 3rd, Minor 6th, Minor 2nd, and likewise finishing with the tritone interval.
Using this formula, you can easily see what the intervals are between the main note and the other notes.
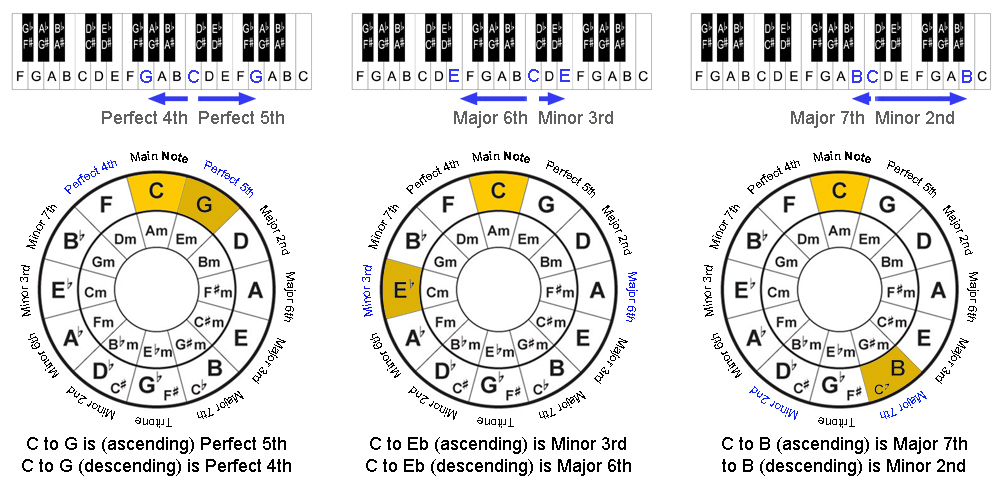
For instance, in the example where C is your main note, you can see that the interval from C to G is a Perfect 5th, the interval from C to Eb is a Minor 3rd, and from C to B the interval is a Major 7th.
Likewise, in the diagram on the right, you rotate the interval circle clockwise to make D your main note. Now you can see that the interval from D to A is a Perfect 5th, the interval from D to F is a Minor 3rd, and the interval from D to Db is a Major 7th.
Using the Circle of Fifths to find Reciprocal Intervals
In the examples above, you’re counting intervals in ascending order from the main note to a higher-pitched note.
Regardless if you’re counting counter-clockwise to find your intervals from C to F, Bb, Eb, Ab, and D, or you’re counting clockwise to find your intervals from C to G, D, A, E, the respective interval names are all in ascending manner.
When you’re going from a lower-pitched note to a higher-pitched note, it’s called an ascending interval.
You can also go the other way in descending order, from a higher pitch to a lower pitch. This is called a descending interval, or Reciprocal Interval.
To find the Reciprocal Intervals for each note from C, you’ll need to look at the circle in halves.
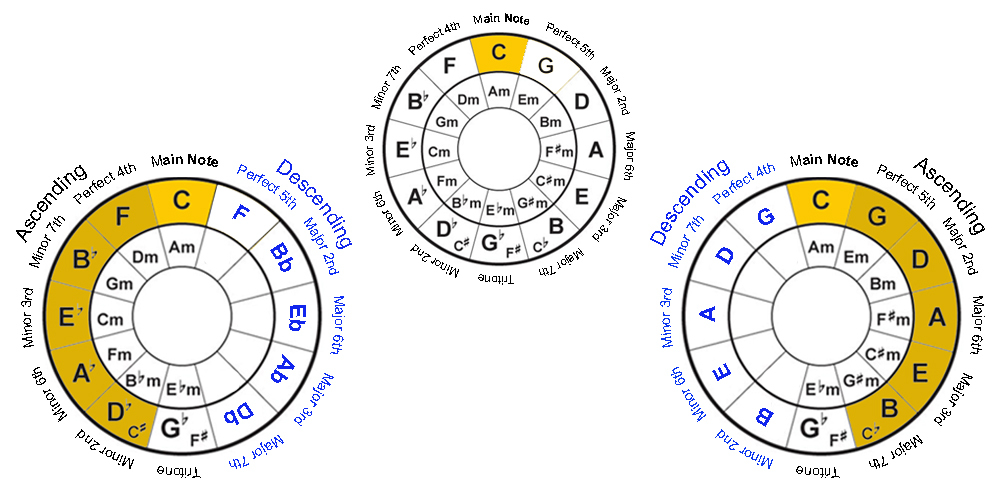
Starting with the left, in ascending order, the interval from C to F is a Perfect 4th. To find the interval of C to F in descending order, just refer to the reflected position on the right side. You’ll see that it’s a Perfect Fifth. That’s your inversed (reciprocal) interval from C to F.
Likewise, the interval from C to Eb in ascending order is a Minor 3rd. By applying the same logic, the interval from C to Eb in descending order is a Major 6th.
Now let’s look at the right side of the circle. The interval from C to G in ascending order is a Perfect 5th. Apply the same inversion logic, you now know the interval from C to G in descending order is a Perfect 4th.
What about from C to E?
In ascending order the interval from C to E is a Major 3rd. On the mirrored side on the left, you now know that the interval from C to E in descending order is a Minor 6th.
To learn more about intervals in detail, check out the videos in the related resources below.
Well, I hope by now, even without fully memorizing the Circle of Fifths, you can at least understand how useful it can be. Especially when you want to acquire certain information right away, you can easily work it out by using the Circle Fifths.
Keep practicing, try to draw out the Circle of Fifths (on paper, or in your mind) using the Order of Sharps and Flats and you’ll have a very powerful tool at your fingertips.
Rock On lnnl,
Related Resources:
Modes Explained Effective and Crystal Clear (Guitar Tutorial with Examples)
Interval Numbers – Intervals Made Easy (Part 1-7) – Easy Music Theory








